MAMANI LOPEZ LILIAN MARCELA: septiembre 2012

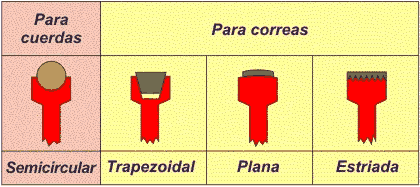
Las poleas son ruedas que tienen el perímetro exterior diseñado especialmente para facilitar el contacto con cuerdas o correas.
En toda polea se distinguen tres partes: cuerpo, cubo y garganta.

El cuerpo es el elemento que une el cubo con la garganta. En algunos tipos de poleas está formado por radios o aspas para reducir peso y facilitar la ventilación de las máquinas en las que se instalan.
El cubo es la parte central que comprende el agujero, permite aumentar el grosor de la polea para aumentar su estabilidad sobre el eje. Suele incluir un chavetero que facilita la unión de la polea con el eje o árbol (para que ambos giren solidarios).
La garganta (o canal ) es la parte que entra en contacto con la cuerda o la correa y está especialmente diseñada para conseguir el mayor agarre posible. La parte más profunda recibe el nombre de llanta. Puede adoptar distintas formas (plana, semicircular, triangular...) pero la más empleada hoy día es la trapezoidal.

Las poleas empleadas para tracción y elevación de cargas tienen el perímetro acanalado en forma de semicírculo (para alojar cuerdas), mientras que las empleadas para la transmisión de movimientos entre ejes suelen tenerlo trapezoidal o plano (en automoción también se emplean correas estriadas y dentadas)

Utilidad

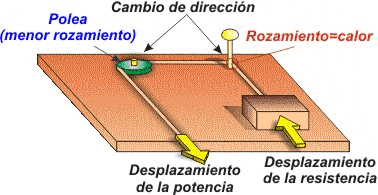
Básicamente la polea se utiliza para dos fines: cambiar la dirección de una fuerza mediante cuerdas o transmitir un movimiento giratorio de un eje a otro mediante correas.

En el primer caso tenemos una polea de cable que puede emplearse bajo la forma de polea fija, polea móvil o polipasto. Su utilidad se centra en la elevación de cargas (pastecas, grúas, ascensores...), cierre de cortinas, movimiento de puertas automáticas, etc.

Polea fija de cable para cambios de dirección

Polea fija de cable para elevación de cargas

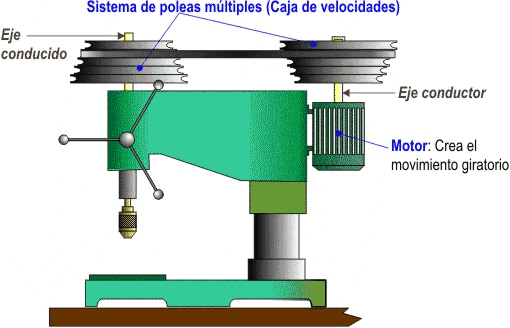
En el segundo caso tenemos una polea de correa que es de mucha utilidad para acoplar motores eléctricos a otras máquinas (compresores, taladros, ventiladores, generadores eléctricos, sierras...) pues permite trasladar un movimiento giratorio de un eje a otro. Con este tipo de poleas se construyen mecanismos como el multiplicador de velocidad, la caja de velocidad y el tren de poleas.

Las poleas se pueden clasificar de la siguiente manera:
POLEAS SIMPLES: esta clase de poleas se utiliza para levantar una determinada carga. Cuenta con una única rueda, a través de la cual se pasa la soga. Las poleas simples direccionan de la manera más cómoda posible el peso de la carga.
polea de tipo simple

Existen dos tipos de poleas simples:

POLEAS FIJAS: consiste en un sistema donde la polea se encuentra sujeta a la viga. De esta manera, su propósito consiste en direccionar de forma distinta la fuerza ejercida, permitiendo la adopción de una posición estratégica para tirar de la cuerda. Las poleas fijas no aportan ningún tipo de ventaja mecánica. Es decir, la fuerza aplicada es igual a la que se tendría que haber empleado para elevar el objeto sin la utilización de la polea.

Sistemas de poleas

Una polea es una rueda que tiene un ranura o acanaladura en su periferia, que gira alrededor de un eje que pasa por su centro. Esta ranura sirve para que, a través de ella, pase una cuerda que permite vencer una carga o resistencia R, atada a uno de sus extremos, ejerciendo una potencia o fuerza F, en el otro extremo. De este modo podemos elevar pesos de forma cómoda e, incluso, con menor esfuerzo, hasta cierta altura. Es un sistema de transmisión lineal puesto que resistencia y potencia poseen tal movimiento.
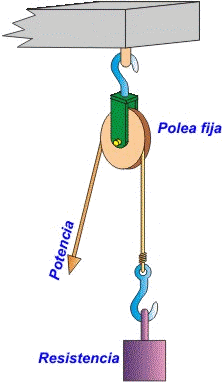
Podemos distinguir tres tipos básicos de poleas:

a) Polea fija: Como su nombre indica, consiste en una sola polea que está fija a algún lugar. Con ella no se gana en Fuerza, pero se emplea para cambiar el sentido de la fuerza haciendo más cómodo el levantamiento de cargas al tirar hacia abajo en vez de para arriba, entre otros motivos porque nos podemos ayudar de nuestro propio peso para efectuar el esfuerzo. La fuerza que tenemos que hacer es igual al peso que tenemos que levantar (no hay ventaja mecánica) F=R. Así, por ejemplo, si deseo elevar una carga de 40 kg de peso, debo ejercer una fuerza en el otro extremo de la cuerda de, igualmente, 40 kg.

Polea móvil

b) Polea móvil: Es un conjunto de dos poleas, una de las cuales es fija, mientras que la otra es móvil. La polea móvil dispone de un sistema armadura-gancho que le permite arrastrar la carga consigo al tirar de la cuerda. La principal ventaja de este sistema de poleas es que el esfuerzo que se emplea para elevar la carga representa la mitad del que haría si emplease una polea fija. Así, por ejemplo, si quisiera elevar una carga de 40 kg de peso, basta con ejercer una fuerza de tan sólo 20 kg.

Polea móvil con una sóla polea

Esto supone que la cuerda que emplee para este mecanismo pueden ser la mitad de resistentes que en el caso anterior. Sin embargo, presenta una desventaja: El recorrido que debe hacer la cuerda para elevar la carga una altura determinada (h) debe ser el doble de la altura buscada (2h).
Aunque consta de dos poleas, en realidad se puede construir este mecanismo con una sola polea (observa la imagen de la derecha). Para ello se debe fijar un extremo de la cuerda, la carga a la polea y tirar de la cuerda de forma ascendente. Precisamente, este es la desventaja, mientras que en el caso de emplear dos poleas, este problema desaparece.
c) Sistemas de poleas compuestas: Existen sistemas con múltiples de poleas que pretenden obtener una gran ventaja mecánica, es decir, elevar grandes pesos con un bajo esfuerzo. Estos sistemas de poleas son diversos, aunque tienen algo en común, en cualquier caso se agrupan en grupos de poleas fijas y móviles: destacan los polipastos:

Poleas de diámetro decreciente y ejes paralelos entre sí que se montan sobre la misma armadura, de modo que existe el mismo número de poleas fijas que móviles.

El extremo de la cuerda se sujeta al gancho de la armadura fija y se pasa alternativamente por las ranuras de las poleas —de menor a mayor diámetro en el caso del polispasto— comenzando por la del grupo móvil y terminando en la polea fija mayor o extrema donde quedará libre el tramo de cuerda del que se tira. La expresión que nos indica el esfuerzo que se debe realizar para vencer una carga (o resistencia) es las siguiente:

siendo n el número de poleas fijas del polipasto. Así, por ejemplo, si disponemos de un polipasto de tres poleas móviles, el esfuerzo que debo realizar para elevar una carga es seis veces menor (2n = 2·3 =6). Suponiendo que la carga sea, por poner un ejemplo, de 60 kg… el esfuerzo que deberíamos efectuar en este caso es de 10 kg.

Otro modelo de polipasto es aquel que emplea dos ramales distintos paralelos y a distinta altura en los que se alojan las poleas. En el ramal superior se sitúan las poleas fijas y en el de abajo las poleas móviles, conjuntamente con la carga.

Por último, es importante señalar que en este tipo de sistema, al igual que la polea móvil, debemos hacer un mayor recorrido con la cuerda; mayor recorrido cuanto mayor es el número de poleas.

Fijas en la siguiente animación. En ella podréis observar como en una polea fija el esfuerzo es idéntico a la resistencia o carga que se desea vencer, mientras que en el caso de una polea móvil tenemos ventaja mecánica, pues el esfuerzo representa la mitad de la resistencia

PROBLEMAS RESUELTOS DE FÍSICA DEL CBC

2.21 - Hallar la intensidad de la fuerza que se debe realizar para mantener en equilibrio un paquete que pesa 120 kgf en los siguientes casos.

Estas cosas se llaman poleas y aparejos. Para analizarlas a todas vamos a tener en cuenta que las cuerdas del CBC (las cuerdas ideales) realizan la misma fuerza en toda su extensión, en particular en sus dos extremos.
Empecemos con la polea simple, caso (a). En este caso la polea tiene la ínica utilidad de desviar la dirección de la soga o, para lo que a nosotros nos interesa, desviar la dirección de la tensión, T, que no es otra que F.

Miremos el DCL correspondiente. Sobre la polea actúan (acá y siempre) tres fuerzas. Dos las ejerce la soga y son iguales. La tercera que actúa sobre el eje de la polea y en este caso se dirige hacia arriba (no necesariamente vertical) no la representé como un vector porque en este caso no nos interesa, termina soportándola el techo, que suele ser todo lo robusto que se necesite.
El hecho de que F y P se ejercen sobre los extremos de una misma soga garantiza que ambas son iguales.

No afecta para nada que una de ellas, F, cambie de dirección. Si analizamos el caso de la derecha vemos que el momento que cada una realiza sobre el eje de la polea tiene el mismo módulo. Concluyendo:

F = P en nuestro caso: F = 120 kgf

(a)

Vamos al caso (b), polea móvil. Al tirar de la cuerda la polea que sostiene la carga sube o baja, por eso recibe su nombre. Es la que está en el medio, va un esquema.

La de arriba de todo no cuenta para nada es una pole fija que hace la tarea más sencilla, pero no modifica el valor de la carga, como vimos en lo anterior.
En la que le sigue, que es la nuestra, aparecen nuevamente 3 fuerzas, las dos que tiran para arriba las hace la cuerda, o sea, F. Y la que tira para abajo es el peso de la carga que deseamos sostener (levantar o bajar, pero en equilibrio). Si le pedimos consejo a Newton nos va a decir:

2F — P = 0

A quien le gusta ver el problema desde el punto de vista del cuerpo extenso (DCL inferior). Como la cuerda está a atada en un extremo al techo se la puede ver como un apoyo. Consideremos a A ese punto de apoyo, luego los momentos de P y F son diferentes. La distancia desde el apoyo hasta P vale R, y hasta F, 2R. Quien lo mira de este modo ve en la polea móvil una palanca del mismo estilo que la carretilla. De cualquiera de las dos maneras obtenemos.

F = P / 2 en nuestro caso: F = 60 kgf

(b)

Ahora viene el arreglo (c), aparejo potencial. Como siempre tememos la polea de arriba que facilita las cosas pero no modifica la carga. Y luego aparecen 3 (podrían aparecer n) poleas móviles enganchadas sucesivamente.

Tal vez te percates que no son igual de móviles (la de abajo se desplaza menos que la de arriba), pero eso es un detalle, no te preocupes. Lo que sí es relevante es que el aparejo éste funciona con cuerdas diferentes, y cada cuerda hace una fuerza diferente al resto.
Para remarcar esa condición importante te dibujé cada cuerda de un color diferente (no fue por una reminiscencia de mi jardín de infantes). Las fuerzas que hacen las diferentes cuerdas las voy a llamar así: cuerda azul, T_A, cuerda roja, T_R, y cuerda verde, lógicamente, F.
Veamos qué pasa polea por polea. En la 1

2T_A = P

en la polea 2

2T_R= T_A

y en la 3

2F = T_R

Combinamos las tres ecuaciones (es un juego de niños) y nos queda:

2 . (2 . (2 . F)) = P

F = P / 2ⁿ en nuestro caso: F = 15 kgf

(c)

Y ahora viene las estrella de la ingeniería, el aparejo factorial. Es el más popular de todos y se usa mucho en la industria y la navegación. Generalmente es el peor interpretado por los estudiantes, y no es culpa de ustedes. Las explicaciones (sobre todo las representaciones gráficas) suelen ser deficientes. Si lo quieren hacer sencillo introducen cuerdas que se doblan (?) como en nuestra guía, o aparejos con poleas de tamaños diferentes que no se ven en ninguna parte más que en los libros de física, y todos meten fuerza irreales entre las poleas que complican la situación. Yo te lo voy a plantear diferente. Primero te voy a mostrar el esquema que hice yo. Es de tipo realista, es el que los otros autores le huyen porque al lector se le arma un bollo de cuerdas en el que se queda enredado. Pero yo te tengo fe. Y además te voy a hacer una propuesta muy, pero muy práctica.
Primero mirá el esquema. Te lo hice en tres partes, rotándolo de a poco para que lo puedas ver por alrededor. Me llevó 1 hora hacerlo. Dedicale 1 minuto.

Como ves tiene una sola cuerda, que se enhebra varias veces por cada conjunto de poleas. La fuerza que hace esa cuerda, no es otra que F, la que tendrá que hacer el operario (o el navegante).
Hay dos conjuntos de poleas. Suelen ser idénticos. Las de arriba juegan el papel de poleas fijas, y ya sabés qué hacen y qué no hacen.
El conjunto de abajo es el que interesa. Las poleas que lo forman juegan el rol de las poleas móviles y ahí está el secreto. Para resolverlo tengo un método muy sencillo. Me parece que es original, porque no recuerdo haberlo visto nunca.

Te propongo que mires solamente el aparejo inferior. Acá te agrego un DCL propio para que no te confundas

Ok, ahí está. Ahora consideralo (no es demasiado imaginativo lo que te pido) un cuerpo único, sólido, bonito... y eso sí, de masa despreciable, como siempre. Y contestame sin titubear: ¿no son seis los trozos de cuerda que salen hacia arriba? ¡Claro! Dos por cada polea del conjunto. Seis cuerdas, igual a 6 F. ¿Y para abajo? ¡Una sola! la carga que queremos sostener, o sea P. ¿Qué diría Newton en este caso? Newton diría...